任何一種理論都有一個發展的過程,並非一帆風順的。起初有人問艾略特,為什麼一個升勢或者一個跌勢必然由五浪組成?而相應的調整由三浪組成?艾略特不知所措,他回答說,這個問題好比“人的手和腳為什麼有五個趾頭”是很難解釋的,因為它是一種自然現象。筆者從圖表裡所觀察的同樣是一種現象,一種規律,而很多現象和規律都是無法解釋的。
艾略特發現費邦納基數列和黃金比率
儘管如此,艾略特不會知難而退,反而更加勇敢,孜孜不倦地去尋求答案。終於,他從哥連斯送給他的資料裡面找到了費邦納基數列,以及由它衍生出來的黃金比率,把它們作為波浪理論的數學基礎。這個數列是中世紀數學家費邦納基(Fibonacci)在回答皇帝的問題時產生的。 (本篇後半部分將有更詳細的介紹。)
費邦納基數列(Fibonacci Sequence)的基本形式為:1,1,2,3,5,8,13,21,34,55,89,144······
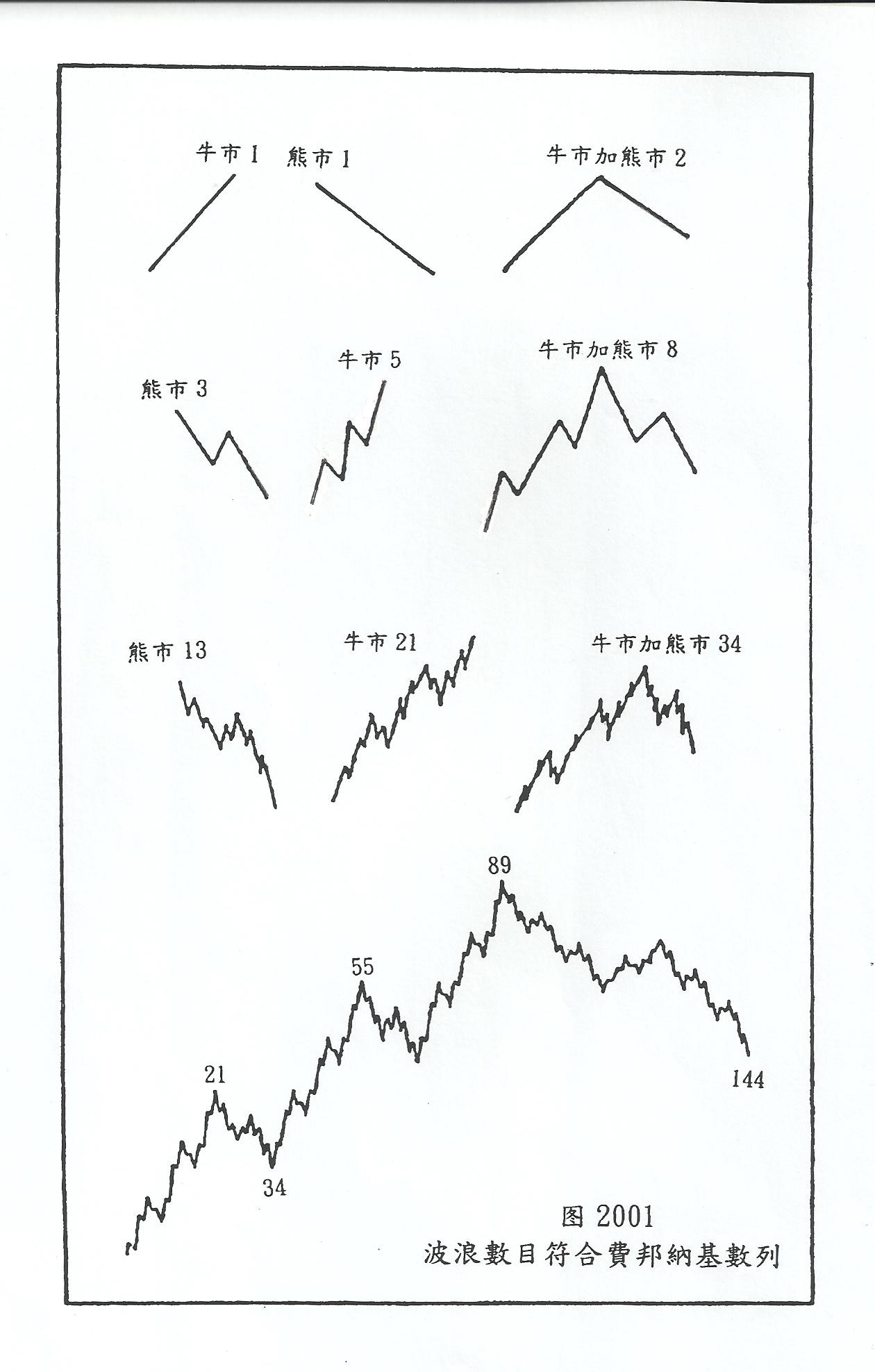
A)波浪數目符合費邦納基數列
我們可以發現,自然界的很多事物離不開費邦納基數列。例如松樹的年輪是5個朝一個方向,8個朝另一個方向,菠蘿釘是8個指著一個方向,13個指著另一個方向。野菊的花瓣是2 1個朝著一個方向,34個朝著另一個方向。向日葵的花瓣是34個指著一個方向,55個指著另一個方向。
艾略特指出,商品價格圖表的波浪數目亦是符合費邦納基數列的。如圖2001所示。 1個熊市加1個牛市等於2個波浪,這兩個波浪完成了一次價格的循環。熊市可分化為3個子浪,牛市可分化為5個波浪,加起來便是8個波浪。同時,我們可以把(a)(b)(c)3個調整浪再分化成13個波浪,亦可以把牛市的5個波浪再分化成21個波浪。按照這種方法繼續分下去,變成34浪、55浪、89浪、144浪,都符合費邦納基數列。這是艾略特把費邦納基數列看做波浪理論依據的第一個原因。
B)波浪長度符合黃金比率
這個數列中相連兩個數字的正比接近0.618 。例如:13÷21≈0.618, 21÷34≈0.618, 34÷55≈0.618 。這個數列中相隔兩個數字的正比接近0.382 。例如:13÷34≈0.382, 21÷55≈0.382 ,34÷89≈0.382。
這個數列中相連兩個數字的反比接近1.618。
例如21÷13≈1.618 ,34÷21≈1.618 ,55÷34≈1.618 。而0.6:1=1:1.618 。
這個數列中相隔兩個數字的反比接近2.168 。
例如55÷21≈2.168 ,89÷34≈2.168 ,144÷55≈2.618 。
再說,0.618×0.618=0.382 ,0.618×1.618=1 ,1.618×1.618=2.618, ,0.382×1.618=0.618 ,0.382×2.618=1 ,1-0.382=0.618 ,0.382+0.618=1 。此外,1÷2=0.5 。這些由黃金比率演變出來的數字,都屬黃金比例的範疇。
我們可以發現,自然界的很多事物存在著這種比率。例如上文提到的松樹年輪、菠蘿釘、菊花瓣、葵花瓣都存在這種比率。人體上,由腳底到肚臍的距離是全身高度的0.618(平均比例)。人的面部,由下巴到眼睛的距離是整個面部長度的0.618(平均比率)。故此,0.618的比率十分容易被人類所接受。
日常生活中,凡是用0.618比率製造的東西能夠讓人類的眼睛格外舒服。故埃及的金字塔、古希臘神殿、維納斯女神、以及現代的鏡框、撲克牌,多采用0.618的比率。華羅庚的優選法,亦採用0.618的或然率。所以這個珍貴的比率被譽為黃金比率
艾略特同時發現,波浪與波浪的長度比例,通常符合0.382,0.5、1、1.618、2.618的比率。後來投資界把黃金比率擴大至0.146、0.236、0.382、0.5、0.618、0.764、1、1.618、2、2.618、4.236等。
這是艾略特認為他找到理論根據的第二個理由
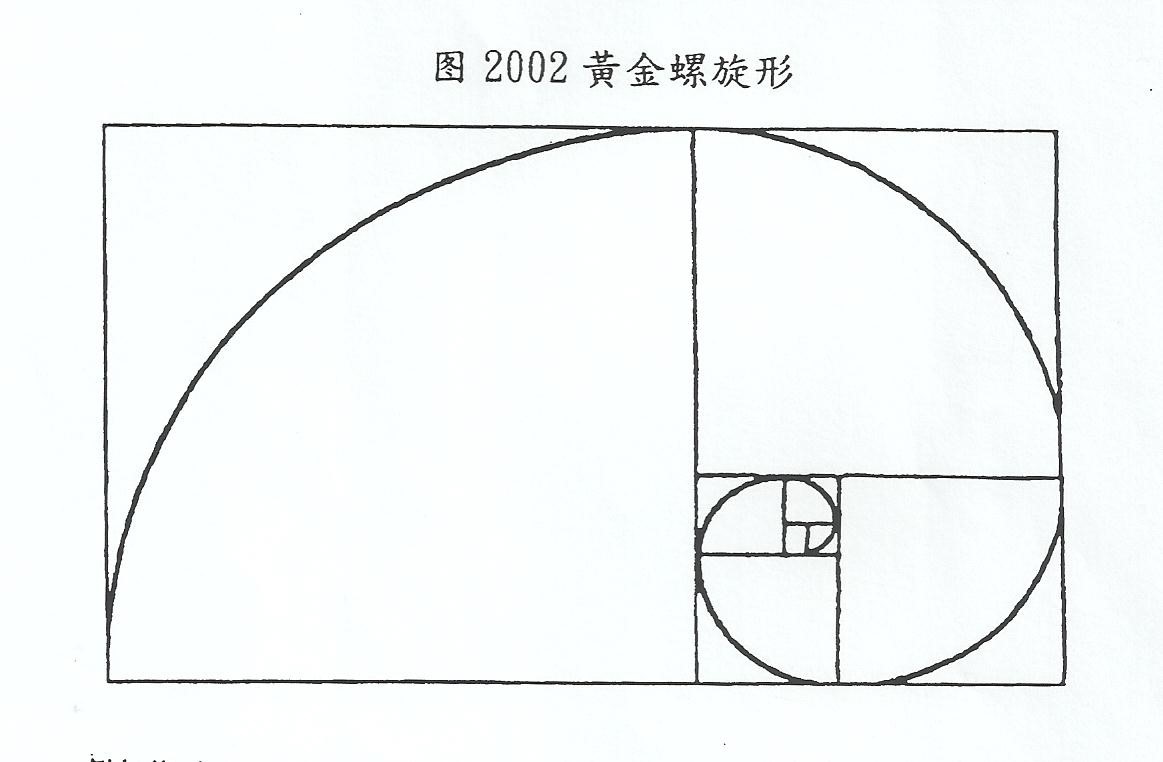
C)長期走勢圖符合黃金螺旋形
艾路特根據0.618的比率繪製成一個黃金螺旋形(如圖2002中所示)。他發現自然界的很多物體都和這個黃金螺旋形相吻合。
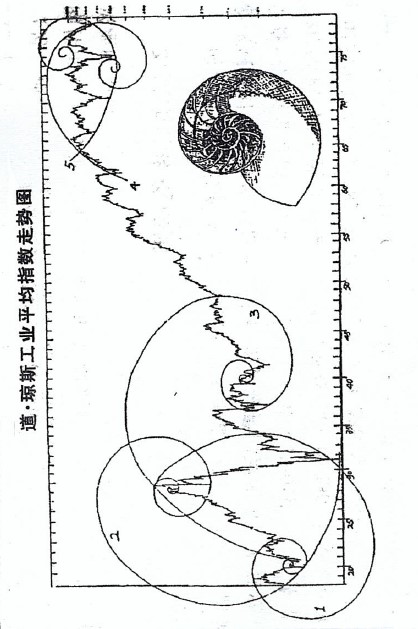
例如蝸牛和螺殼的形狀,海馬的尾巴、山羊的捲角、天然的蜂巢、海浪和漩渦的形狀、松果、以至天上星星的排列,都與黃金螺旋形相吻合。人類的耳朵構造,亦是一個黃金螺旋形。艾略特把黃金螺旋形放到較長期的圖表走勢中,發現常常起到支持和阻力作用,故而更加肯定圖表走勢中存在黃金比率。 (作者按:黃金螺旋的製作方法將在本篇後半部分介紹。)


卷起的波浪

基於以上的理由,艾略特認為自己已經找到答案,即把費邦納基數列和黃金比率作為波浪理論的數字基礎。作為波浪理論的哲學基礎。可是後來人們發現,費邦納基數列與黃金比率,它們和金融圖表之間並沒有必然的關係,只屬偶然的現象。故而認為艾略特只是找到一個數學基礎,而非哲學基礎!